admin 随着加解密技术研究的不断深入和混沌学的继续发展，低维度混沌序列加密已经出现了一些破解攻击方法，信息的安全得不到保证。高维度混沌因为具有高周期性，更好的随机性和大复杂度，可以提供更好的加密效果，更好地保证图像信息的安全性，因此结合高维度混沌序列的加密算法成为研究热点。我们在研究二维Henon映射和三维Rossler混沌映射的基础上，提出了一种基于Henon映射和Rossler混沌映射的数字图像加密算法。
一、 Henon映射
典型的二维Henon映射离散非线性动力系统：
其中α，β为系统参数。当α=1.4，β=0.3，系统(1)处于混沌状态。此时，最大Lyapunov指数等于0.418。当β=1时，系统在运动中保持相平面积不变，描述的是保守系统：当β<1时，系统在运动中相平面积缩小，是耗散系统。大量的研究表明，在非线形耗散系统中有混沌并伴有混沌吸引子，在非线形保守系统中也有混沌，只是没有混沌吸引子。
二、Rossler混沌映射
Rossler系统是非线性动力学中最有名的方程之一，有着广泛的物理背景和工程背景。三维Rossler混沌映射的动力学系统模型如下：
其中a，b，c为系统参数。当a=0.2, b=0.2，c=5.7时，系统(2)处于混沌状态。
在加密系统中，Rossler混沌映射与低维混沌映射相比有如下特点：
(1)系统结构更为复杂，因此由此生成的实数序列更难以预测，使得其应用极为灵活；
(2)实际应用中，低维混沌系统会出现周期退化问题，因此容易受到系统模型重构的攻击，而高维混沌系统其运算掩盖了混沌子序列的分布特性，改变了混沌系统的动力学行为，能够有效抵抗模型重构的攻击；(3)由于对初始值敏感，而初始值基本上是无精度的，因此密钥空间远远大于低维系统。
Rossler混沌映射是一个偏微分方程组，因此在应用到图像加密系统之前先要将其离散化转变为实数序列。利用Euler法或四阶经典Runge-Kutta方法（简称RK法）求解出Rossler方程组的实值解是目前较常用的两种方法。 RK方法因为求解精度相对较高，因此本文采用的是四阶经典RK方法求解Rossler混沌映射方程组解。
三、基于Henon映射和Rossler混沌映射的加密算法
本文提出的基于Henon映射和Rossler混沌映射的数字图像异或加解密算法是一种置换型的图像加密算法，经过两次加密后图像中的各像素值都由新的像素值所替换，使得加密后图像的像素分布发生变化。记原始图像为明文矩阵On，由Henon映射和RossLer混沌映射的离散化产生的实数序列为{Kn}，相应的密钥矩阵为Cn，加密后的图像密文矩阵为En，选取Henon映射的初始值组[U0，Vo]作为数字图像一次加密的密钥组；选取Rossler混沌映射中的初始值组[Xo，Yo，Zo]以及RK算法中的控制变量步长h-起构成数字图像二次加密的密钥组[Xo，Yo，Zo，h]；选取BMP格式图像来论述该算法。
1、基于Henon映射和Rossler混沌映射的异或加密算法
基于Henon映射和Rossler混沌映射的异或加密算法过程如下：
(1)打开原始的BMP图像文件，顺序读取图像中各点像素值，得到原始图像的像素矩阵On；
(2)根据Henon映射方程，输入混沌系统的参数α，β和初始条件U0，Vo，作为图像一次加密密钥，生成Henon混沌加密序列{Ku}，{Kv}；
(3)将{Ku}，{Kv}混沌序列值乘以256，然后取整数部分作为新的序列值，再分别各自重新组成和原始图像同样大小的矩阵Cu，Cv；
(4)将矩阵Cu，Cv中的元素与原始图像的像素矩阵On。先后做按位异或处理，即通过式子En=On+Cu+Cv，获得Henon加密后的图像矩阵En；
(5)根据原始图像大小，选取Rossler混沌映射的密钥组[Xo，Yo，Zo，h]，通过RK法求解出与原始图像像素个数相同的Rossler混沌映射的离散化实数序列{Kx}，{Ky}，{Kz}；
(6)先分别取出序列{Kx}，{Ky}，{Kz}中各值的小数部分乘以256，然后取乘积结果的整数部分，再将每个元素转化为8位二进制数，最后分别各自重新组成和原始图像同样大小的矩阵Cx，Cy，Cz；
(7)将新矩阵Cx，Cy，Cz中的元素与Henon一次加密后的图像矩阵En中的相应元素做按位异或处理，即按照式子
进行处理，处理后得到Rossler混沌映射二次加密的
图像矩阵En'；
(8)将矩阵En'。按照图像标准格式不经压缩地保存下来，即为需求的最终加密图像。
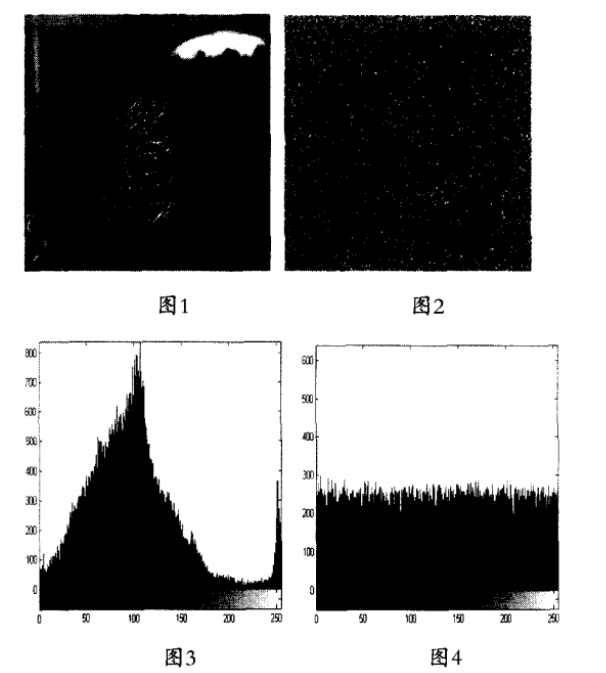
图1为“微上理”原始图像，图2显示的是经过两次加密后得到的加密图像效果图。其中Henon映射一次加密时所选取的初始值组为[0.39895，0.40102]，Rossler混沌映射二次加密时所选取的密钥组为[0.98786，1.01023，0.99785，0-01]。通过比较图1和图2可以看出：加密后的图像变得杂乱无章，面目全非，无法从中读取任何信息。这样就对原始图像所包含的信息进行了有效的保护。图3是原始图像的直方图；图4是二次加密后图像的直方图。通过比较图3和图4可以看出图像文件加密后的每个像素点分布得更加均匀，充分说明该算法是一种置换型加密算法，并且具有很好的加密效果。
四、基于Henon映射和Rossler混沌映射的解密算法
解密算法是加密算法的逆运算，其主要步骤如下：
(1)打开加密图像文件，顺序读取图像中各点像素值，得到加密图像的像素矩阵En'；
(2)利用加密时使用的Rossler混沌映射的密钥组，根据加密图像大小通过RK法求解出与其像素个数相同的RossLer混沌映射的离散化实数序列{Kx}，{Ky}，{Kz}；
(3)先分别取出序列{Kx}，{Ky}，{Kz}中各值的小数部分乘以256，然后取乘积结果的整数部分，再将每个元素转化为8位二进制数，最后分别各自重新组成和原始图像同样大小的矩阵Cx，Cy，Cz；
(4)将新矩阵Cx，Cy，Cz中的元素与加密图像的像素矩阵On中的相应元素分别做按位异或处理，即按照式
进行处理，得到Rossler混沌映射解密后的新矩阵On'；
(5)根据Henon映射方程，输入混沌系统的参数α，β和初始条件U0，Vo，作为图像二次解密密钥，生成Henon混沌解密序列{Ku}，{Kv}；
(6)将{Ku}，{Kv}混沌序列值乘以256，然后取整数部分作为新的序列值，再分别各自重新组成和原始图像同样大小的矩阵Cx，Cy，Cz；
(7)将矩阵Cu，Cv中的元素与步骤(4)得到的Rossler混沌映射解密后的矩阵On'。先后做按位异或处理，即通过式子
，处理后获得Henon二次解密后的图像矩阵On；
(8)将矩阵On按照图像标准格式不经压缩地保存下来，即为需求的最终解密图像。
对图2所示的加密图像进行解密，得到正确解密的图像如图5所示。将图1和图5所示的两幅图像进行按位异或处理，得到一幅像素值全为0的全黑图像如图6所示，表明解密得到的图像与原始图像完全一样，也证明解密是无损的。
五、基于Henon映射和Rossler混沌映射的数字图像加密安全性分析
整个算法的安全性通过以下两个方面来进行分析：
(1)密钥有效精度：
由于二维Henon映射和三维Rossler混沌映射不仅具有对初值极度敏感的特性，使混沌系统更为复杂，并且扰乱了动力系统中的运动行为，所以只要选取的解密密钥组与加密密钥组有任何细微的区别，都不可能正确解密加密图像，并对系统模型重构攻击有很强的免疫力。理论上密钥组的精度是没有限制，但受到实际操作中计算机精度的限制，如果使用的计算机精度越高，则密钥空间就越大。
(2)像素有效位：
在进行按位异或操作之前，每个像素值都要转化为8位二进制数，因此精确解密一个像素值要进行大概255次操作。如果要精确解密一个大小为M×N的矩阵用本文提出的加密算法进行加密的数字图像，则大概需要尝试(255M+N)5次。
因为Henon映射和Rossler混沌映射都是混沌系统，因此混沌系统具有的生成值空间数目众多并且互不相关、对初值极度敏感等特性二者都具备。又因为Rossler混沌映射属于高维混沌系统，具有更好的随机性和更强的对模型重构攻击抵抗性，同时具有比低维混沌系统更好的复杂性，也容易产生出保密性更好的密钥空间，能够用在数字图像加密和解密中，产生具有安全性更高的密码系统。
小知识之Lyapunov指数
Lyapunov指数是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。对于系统是否存在动力学混沌, 可以从最大Lyapunov指数是否大于零非常直观的判断出来: 一个正的Lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。
