圆锥曲线加密算法是一种新型的公钥加密算法,其参数选择会直接影响加密算法的安全性。那么接下来我就给大家简单的介绍一下圆锥曲线公钥加密算法的参数选择。
一、有限域Fp上圆锥曲线的参数选择
1、有限域Fp上的圆锥曲线
有限域Fp上的圆锥曲线Cp(a,b)是指同余方程:
![]() 其中,p是奇素数。将y ≡ xt (mod p)代入式(1),则圆锥曲线Cp(a,b)的全部点表示为
其中,p是奇素数。将y ≡ xt (mod p)代入式(1),则圆锥曲线Cp(a,b)的全部点表示为
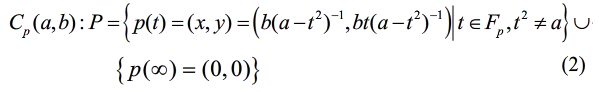
其中,(a – t 2)–1为(a – t 2)在有限域Fp上的乘法逆元。Cp(a,b)上,定义如下运算规则:
(1)加法运算⊕:
1)对于P = p(t) ∈ Cp(a,b),满足p(t) ⊕ p(∞) = p(∞) ⊕ p(t) = p(t)。
2)设P1 = p(t1), P2 = p(t2), P3 = p(t3)且t1, t2 ≠ ∞,定义p(t1) ⊕ p(t2) = p(t3)。
其中,
![]() (2)点P的逆元:
(2)点P的逆元:
记作–P,当P = p(t)时,则:
![]()
(3)标量乘运算*:
k为整数且P = p(t) ∈ Cp(a,b),记 :
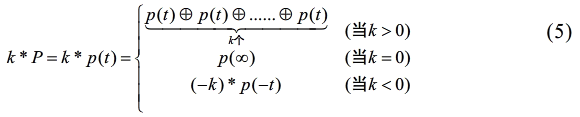
目前已有资料证明了圆锥曲线(Cp(a,b), ⊕)的点和运算构成群,利用圆锥曲线群(Cp(a,b), ⊕)可构造基于离散对数的密钥交换协议和公钥密码系统的方法,如Diffie-Hellman密钥交换协议、ElGamal加密方案、Massey-Omura加密方案等。在加密操作过程中,需要将明文m表示为圆锥曲线Cp(a,b)上点(即明文嵌入),编码算法为xm = b(m 2 + m + a)–1, ym = bm(m 2 + m + a)–1,在解密操作过程中,译码算法为m = ym xm–1。
二、参数选择与安全性
在式(1)所定义的圆锥曲线方程Cp(a,b)中包含两个参数,它们的选择范围和圆锥曲线加密算法安全性的关系为 :
(1)参数b:
由于该参数仅在明文嵌入与译码中起作用,因此其取值对于圆锥曲线的安全性不会产生任何影响。
(2)参数a:
由于该参数涉及到圆锥曲线群上的计算,其取值直接影响到圆锥曲线加密体制的安全性,因此需要进行讨论。
1)当a为有限域Fp上的二次剩余,即当Legendre符号(p/a)=1时,通过构造映射,设θ1和θ2为模p的二次剩余a的两个根(其中θ1 ≠ θ2),在已知θ的情况下可以构造从有限域Fp上的圆锥曲线群(Cp(a,b),)⊕到有限域Fp上的普通乘法群(Zp ,*)的映射:
![]()
其中,θ12 = θ22 = a。
经过式(6)映射后,有限域Fp上的圆锥曲线群的离散对数的安全性被降低到有限域Fp上的乘法群上的离散对数问题的安全性。特别地,当a为有限域Fp上的二次剩余且θ为a的二重根时,不仅可按照式(6)构造从圆锥曲线群(Cp(a,b),)⊕到有限域Fp上的乘法群(Zp ,*)的映射,还可以按照式(7)构造从有限域Fp上的圆锥曲线加群(Cp(a,b),)⊕到有限域Fp上的普通加法群(Zp,+)的映射:
![]()
其中,θ2 = a。
经过式(7)映射后,有限域Fp上的圆锥曲线群的离散对数的安全性被降低到有限域Fp上的普通加法群上的离散对数问题的安全性。此时圆锥曲线上的标量乘运算可以通过域上的乘法运算求解,因而可通过域上的除法计算求解任意点的逆元。从而使得定义在该圆锥曲线上的加群(Cp(a, b), )⊕变得毫无安全性可言。
2)当a不是有限域Fp上的二次剩余,即在Fp域上不存在a的平方根θ使θ2=a时,此时需通过扩域才有可能在规模至少是有限域2pF的域上构造与圆锥曲线群(Cp(a, b),)⊕同构的普通乘法群。由于有限域2pF上操作数的长度比有限域Fp上操作数的长度多了一倍,因此,此时构成的映射并未降低原有限域Fp上的圆锥曲线离散对数的安全性。
综上所述,为了保证圆锥曲线公钥密码体制的安全性,需要取适当的a值,从而使![]() ,即在有限域Fp上a不是模p的二次剩余,二次剩余的判定可通过Euler判别法计算。参数a的取值算法具体描述如下:
,即在有限域Fp上a不是模p的二次剩余,二次剩余的判定可通过Euler判别法计算。参数a的取值算法具体描述如下:
算法 有限域Fp上产生圆锥曲线参数a的算法。
输入 模p的取值。
输出 适当的a值。
步骤1 随机取适当的a值;
步骤2 计算![]() ;
;
步骤3 若![]() 返回步骤1;
返回步骤1;
步骤4 得到适当的a值,算法结束。
2、环Zn上圆锥曲线的参数选择
环Zn上的圆锥曲线Cn(a,b) 是指同余方程:
![]() 其中,p,q为两个不等的奇素数;n= pq。模n下的加、减、乘法运算构成了环Zn上的运算,根据式(3)可得到Cn(a, b)上的点,并通过在Cn(a, b)的点上定义加法运算⊕,从而得到环Zn上的圆锥曲线群(Cn(a, b),)⊕。其中,环Zn中加法运算⊕的定义类似于式(2)~式(5)。
其中,p,q为两个不等的奇素数;n= pq。模n下的加、减、乘法运算构成了环Zn上的运算,根据式(3)可得到Cn(a, b)上的点,并通过在Cn(a, b)的点上定义加法运算⊕,从而得到环Zn上的圆锥曲线群(Cn(a, b),)⊕。其中,环Zn中加法运算⊕的定义类似于式(2)~式(5)。
对于环Zn上的圆锥曲线(Cn(a,b), )⊕的应用,如利用环Zn上的圆锥曲线对RSA公钥密码体制进行模拟。若按照式(6)构造从环Zn上的圆锥曲线群到环Zn上的乘法子群的映射,则必须要在环Zn上计算参数a的二次剩余。当合数n为两相异素数p, q的乘积时,对于模n的二次剩余问题有:
(1)在未知n的分解的情况下,模n的二次剩余判定问题(QRP)是一个数学难题。
(2)分解n的计算等价于求模n的平方根。
由此可见,当合数n的分解未知时,在环Zn中无论是二次剩余的判断问题还是平方根的求解问题都是困难的。因此,构造从环Zn上的圆锥曲线群到环Zn上的乘法子群的映射是困难的。 综上所述,当圆锥曲线建立在环Zn上时,为了避免安全上的漏洞,提高运算的安全性,对于参数a的取值可选择如下两种情况,其中的(a/p)或(a/q)可通过Euler判别法计算:
![]() 此时,Jaccobi符号
此时,Jaccobi符号![]() 。根据Jaccobi符号的概念可知,当Jaccobi符号结果为–1时,在环Zn中不存在a的二次剩余。
。根据Jaccobi符号的概念可知,当Jaccobi符号结果为–1时,在环Zn中不存在a的二次剩余。
![]() 尽 管 此 时Jaccobi符 号
尽 管 此 时Jaccobi符 号![]() ,但在环Zn中并不存在a的二次剩余。
,但在环Zn中并不存在a的二次剩余。
三、扩展的圆锥曲线及其参数选择
在特征char(F)=2的有限域上,任何元素t与2的标量乘2*t=t+t=0,其中,0指char(F)=2的有限域域中的零元。由式(5)可知,当t1 = t2 = t ≠ ∞且t1 + t2 ≠ 0时,p(t3) = 2*p(t) = p((t2+a)(2t)–1)。特别地,在特征char(F)=2的有限域上p(t3) = 2*p(t) = p(∞),即在特征char(F)=2的有限域上圆锥曲线群仅存在阶为2的子群。显然,该运算使得圆锥曲线上的离散对数运算不能够加密任何数据。 为了使圆锥曲线公钥密码体制在特征为2的有限域上实现,将原圆锥曲线的定义方程扩展为式(9)的形式:
![]()
根据圆锥曲线的相关性质,由式(9)推导出特征char(F)=2有限域上的圆锥曲线方程上群的运算:
(1)对于加法运算⊕,有p(t1) ⊕ p(t2) = p(t3),其中:
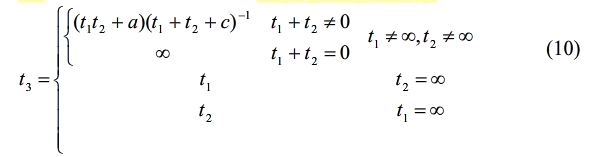
(2)当t≠0且t≠∞时,倍乘运算*为:
![]()
综上所述,改进后的圆锥曲线中增加了参数c,通过改变参数c的取值可以使圆锥曲线公钥密码体制建立在任意特征的有限域上。设t≠0且t≠∞,参数c的取值按如下方式进行产生,
(1)当char(F)≠2时,此时令参数c=0,从而倍乘:
![]()
(2)当char(F)=2时,此时令参数c≠0,从而倍乘:
![]()
通过上述分析可知,有限域Fp和环Zn上圆锥曲线密码算法安全性主要取决于参数a的选择。
小知识之圆锥曲线
圆锥曲线包括椭圆,双曲线,抛物线。其统一定义:到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0<e<1时为椭圆:当e=1时为抛物线;当e>1时为双曲线。









