浅析一种快速分组加密算法——MUST1算法

在信息社会中 ，信息安全本身是财富 ，是时间 ，甚至是生命。如何保护信息的安全不仅仅是各国政府和军方所关心的问题 ，而且所有的企事业单位也同样有迫切需要 。标准密码则是一种有效而可行的方法 。美国的数据加密标准DES在我国的许多领域均被广泛应用 ，但是由于密钥太短而且濒临它的生命尽头 ，并被AES所取而代之 。但AES的基本要求比三重DES快而且至少和三重DES一样安全 ，分组长度为 128bit，密钥长度为128/192/256bit。AES和DES均是美国的数据加密标准 ，直接采用对保护我们国家的信息安全显然是极不适当的 。

于是我们在研究话密时开发出来了一种分组算法——MUST1(Macau University of Science and Technology的缩写 ，1是序号 ) 。同时设计了利用MUST1构造HASH函数的方法 ，同样具有抗攻击能力强 ，效率高的特点 。其算法的软件或硬件实现都极容易 。

MUST1加密算法的描述
MUST1是采用Feistel网络 ，把任何函数转化为一个置换 。即
MUST1(m) =G₈·(I·G₇)·(I·G₆ )·…·(I·G₂ )·(I·G₁) (m)
式中G_i 是图 1的变换 ，即
G_i(L_i- 1，R_i- 1) =(L_i-R_i) 。
其中　L_i=L_i- 1 g(R_i- 1，Sk_i) ，R_i=R_i- 1，
i=1，2 ，… ，8。

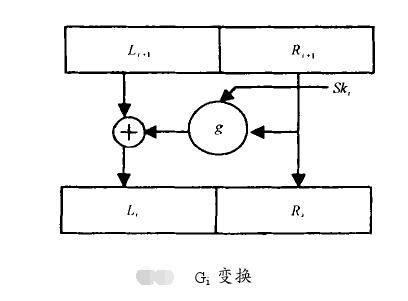
I是变换 ：I(L,R) =(R,L) ，其中L和R都是 64bit。

MUST1算法的核心在于 g(Ri- 1，Ski)的构造 。g(R，Ski) =(I，r) ，其中I，r都是 32bit的 0，1符号串 ，R是 64bit的 0 ，1符号串 。将R分解为I，r两组 ，各32bit。

MUST1的解密
MUST1的解密和加密类似 ，只是子密钥的顺序相反 ，即

子密钥生成
密钥k =k₁ｋ₂ …k₂₅₆ 。
将ｋ向左旋转移位 16bit，设得
h₁⁽¹⁾ｈ₂⁽¹⁾ …h₂₅₆ ⁽¹⁾，
取sk₁= H₁⁽¹⁾ｈ₂⁽¹⁾…ｈ₁₉₂⁽¹⁾ ，再将h₁⁽¹⁾ｈ₂⁽¹⁾ …h₁₉₂⁽¹⁾ 向左旋转移位 16 bit ，设得
h₁⁽²⁾ｈ₂⁽²⁾ …h₂₅₆ ⁽²⁾ ，令
sk₂ = h₁⁽²⁾ｈ₂⁽²⁾…h₁₉₂⁽²⁾ ，
依上述方法产生sk₃，sk₄ ，…sk₈。

用MUST1加密算法构造HASH函数
在网上通信用得很多的确认技术 ，即A向Ｂ用明文形式把信息ｍ送到B。为了让B确保信息如ｍ是由A送来 ，可在ｍ的后面附上固定长度的数码 。B收到后可通过相同的算法及密钥 ，确定接收或拒绝对方信息 。

单向散列函数H（m） ，对一任意长度的信息m ，它返回一固定长度的散列值
h =H(m)。要求满足:
给定m，求h是容易的；
给定h，求m是困难的 ；
给定m，要找另一信息m′ ，并满足H(m) =H(m′)是困难的 。

MUST1算法也可用来产生128bit的散列值 。
设m=m₁m₂ …m_k,m_i 长128bit的分组 ，
i=1,2 ，… ，k；ｋ =k₁ｋ₂ …k₁₂₈k₁₂₉…k₂₅₆。
令
k₁=ｋ₁ｋ₂ …ｋ₁₂₈，
k_r=k₁₂₉ｋ₁₃₀ …ｋ₂₅₆ ，
而
ｋ=k₁·ｋ_r(k₁ 和ｋ_r 连接 ) 。

构造H(m)的算法

HASH函数的图如下图所示 ：

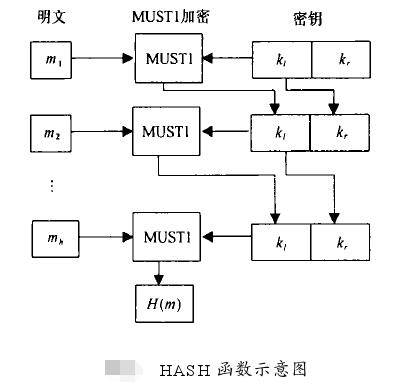
MUST1加密算法是快速高效安全的一种分组加密算法 。用它构造电子HASH函数同样具有抗攻击能力强和效率高的特点 。MUST1的明、密文都是128bit ，密钥长 256bit，大量实验证明其效率高于DES近 3倍 ，密钥长度是DES的 4倍 。MUST1除适用于一般电子信息的保密用途外 ，因具高效及在硬件上易于实现等特点 ，特别适用于实时加密通信的应用 。语音加密通信是我们正在研究的项目之一 ，它以MUST1为核心与电子线路相结合 ，算法以数字密码器为基础 ，存放在单片机中 ，与电话机相连 ，组成语音保密系统

ice普通用户

海报分享