数字图像实值加密方法之分数阶Fourier变换

我们通过构造保实分数阶Fourier变换，提出了一种不同于上述方法的实值数字图像文件加密方法。该加密算子是一个实数域到实数域的映射。本算法利用该变换的保实特性将原始图像映射到由密钥决定的保实分数阶Fourier变换域中，得到实值的密文图像。明文和密文分别处于空域和保实分数阶域上，具有较强的抗统计破译能力。该方法为数字图像文件（尤其是实值图像）加密提供了一个新的解决方案。

一、分数阶Fourier变换

首先简要介绍分数阶Fourier变换，它是一种线性算子，信号的分数阶Fourier变换被定义为：

其中分数阶Fourier变换核Ka（t，u）为：

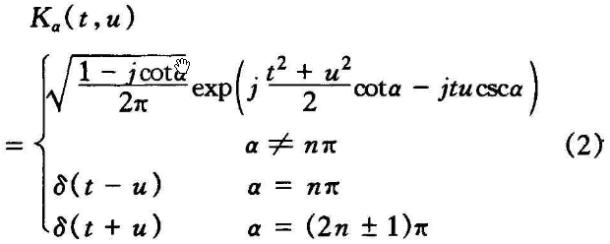
式中：α为分数阶Fourier变换的角度；n为整数。为讨论方便起见，文中使用变换阶数来描述分数阶Fourier变换域，即α=aπ／2，a可以取[0，4]区间内的任意实数。当a= O(α=O)时，变换对应信号本身；当a= 1(α=π/2)时，退化为传统的Fourier变换。可通过阶数为-a的分数阶Fourier变换来实现逆变换。分数阶Fourier变换算子P的变换阶数具有连续可加性：

分数阶Fourier变换的快速算法有很多种，在处理数字图像时，需要使用二维离散算法。二维离散分数阶Fourier变换核具有可分离性，因此可分解成为二次一维分数阶Fourier变换，即分别沿列方向和行方向进行一维分数阶Fourier变换。其张量积的形式为：

式中：Ma为a阶离散分数阶Fourier变换矩阵；为数字图像矩阵。其逆变换为：

这种快速算法的计算复杂度与传统Fourier变换相同，为O(Nlg(N))。

二、基于保实分数阶Fourier变换的数字图像文件加密和解密算法

1、保实分数阶Fourier变换的构造

I Venturini等人提出了一种将任意分数阶变换进行保实化处理的方法，使得构造出毒的保实变换前后数据均为实数，恰好为实值加密问题提供了一个解决途径。本文在此基础上构造了一种保实的分数阶Founier变换。其过程如下：

(1)若x={x1，x2，x3，…，xN}T是长度为N的一维实信号(N为偶数)，首先将其构造为一个长度为N／2的复向量x：

(2)求y=Ma，N/2 gX，其中Ma，N/2是大小为(N/2)×(N/2)的a阶离散分数阶Fourier变换矩阵（下文简写为Ma）。

(3)令y'=(Rey，Imy)T，y'即为对x做a阶保实离散分数阶Fourier变换的结果。

若用实部虚部的计算来描述整个构造过程，有：

所以：

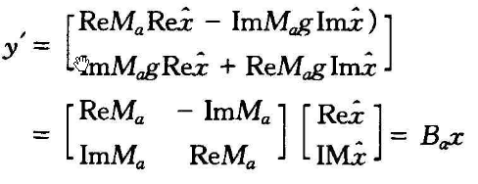
其中：

因此本文构造的a阶保实离散分数阶Fourier变换可表示为：

该保实分数阶Fourier变换是构造出来的，为了获取保实的特性，变换矩阵Ba并没有继承分数阶Fourier变换算子的所有性质，不过还是保持了酉性和变换阶数的连续可加性，同样可以通过负阶数变换来完成逆变换，即Ba-1=B-a。当a从0变到1时，该变换有连续增长的去相关能力。

2、加密算子的定义和具体加密方法

为了将本加密算法用于数字图像文件加密，以便取得更好的安全性，进一步构造了一个N×N的置换矩阵Pkev，它是一个每行每列有且仅有一个非零元素1的方阵，在本加密算法中它由种子key生成。

由此，本文提出的数字图像加密算法的算子定义如下：

式中：Ba的定义与式(6)相同；x是一个长度为N(N为偶数)的实向量。

R(a，key)称为基于保实分数阶Fourier变换的加密算子，并且在置换矩阵种子相同的情况下具有阶数可加性和交换性：

将上述算法推广到二维，利用张量积的形式R（a，key）gXgRTb，key2)来进行二维加密变换，用来处理数字图像。其中a，b是二维变换的两个阶数，key1和key2分别是在两个方向上生成的置换矩阵所用的种子。对数字图像X进行基于分数阶Fourier变换的实值加密方法可表示为：

将算法中用到的四个参数(a，b，key1，key2)看作是广义的密钥，用来控制密文的生成。由算子R(a，key)的交换性和变换阶数可加性可推知，解密过程可使用密钥(-a，-b，key1，key2)，可通过与加密过程相同的流程完成。

综上所述，本算法的实现具体包括如下的步骤(图1)：

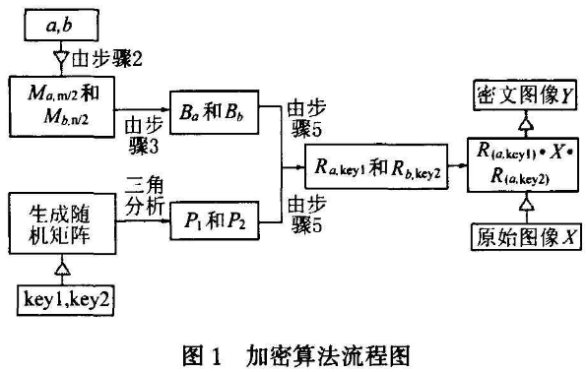
(1)对一幅大小为m×n的灰度图像（其灰度值矩阵为X）设置密钥参数为(a，b，key1，key2)。

(2)由密钥中两个变换阶数a和b计算出相应的m/2点和n/2点离散分数阶Fourier变换矩阵Ma，m/2和Mb，n/2。

(3)根据式(6)计算相应的Ba矩阵和Bb矩阵。

(4)由密钥中两个置换矩阵种子keyl和key2分别产生大小为m×m和n×n的随机矩阵，然后分别对这两个随机矩阵进行LU三角分解，得到所构造的两个置换矩阵P1和P20。

(5)按照式(8)计算相应的加密算子R(a，key1)和R(b，key2)。

(6)按照式(9)对待加密图像矩阵X进行实值加密变换，得到密文图像Y。

(7)解密过程可使用密钥(-a, -b，key1，key2)，通过与加密过程相同的流程完成解密。

3、算法可行性和安全性讨论

下面讨论本算法用于图像加密的可行性。为了信息的保密性，抵抗密码分析，一个保密系统应当满足下述要求。

(1)系统即使达不到理论上是不可破的，也应当是实际上不可破的。也就是说，从截获的密文或某些已知的明文密文对，要决定密钥或任意明文在计算上是不可行的。

(2)系统的保密性不依赖于对加密体制或者算法的保密，而是依赖于密钥的保密。这是著名的Kerchhoff准则。

(3)加密和解密算法适用于密钥空间中的所有元素。

(4)系统便于实现和使用。

经过本文前几部分的叙述可以看出，由密钥确定的保实分数阶Fourier变换图像加密算法可以充分实现明文与密钥的扩散和混淆，它们之间没有简单的关系可循，加之利用变换阶数控制复杂的变换，在已知种子（即密钥的一部分）的情况下从截获的密文反推密钥中的变换阶数是很困难的，只能依靠穷举搜索，这是因为分数阶Fourier变换可看作是一个单向陷门函数，在已知明文密文对的情况下推出所使用的置换矩阵种子和变换阶数也是不可行的，这使得密码分析人员只能使用穷举法进行破译，在本
文下一节的仿真中将会详细说明本文算法的加密效果和安全性，并满足Kerchhoff准则。

此外，本加密算法和解密算法的差别仅仅在于二维分数阶Fourier变换的两个变换阶数a和b的符号，因此可以用同一模块完成加密和解密。分数阶Fourier变换可通过FFT实现快速计算，因而使得本算法易于实现，具有与FFT相比拟的运算速度。由于使用了保实的分数阶Fourier变换，因而加密过程不会产生数据膨胀，密钥简单，可控性强，便于使用。可见，本文提出的基于保实分数阶Fourier变换的图像加密算法是可以作为一个加密系统的。

需要迸一步说明的是，进一步定义的两个参数key1和key2，即构造R(a，key1)和R(b，key2)中置换矩阵的种子，可使得算法具有更加安全的加密效果，置换矩阵P能够隐藏所使用的Ba和Bt,矩阵，因而间接隐藏了变换阶数a和b（图1），并能提供更好的扰乱效果。由不同的种子生成的置换矩阵P不同，得到的密文信息也不同（通过仿真可知同一图像由不同密钥生成的密图是互不相关的），增大了破译的难度，进一步提高了安全性。

通过本文提出的算法对数字图像进行实值加密，密文是在由密钥确定的保实分数阶Fourier域，即明文与密文在不同的变换空间，具有不同的统计特征。仿真发现，密文具有类似白噪声的自相关性，可以抗统计破译。

三、仿真与分析

使用MATLAB软件对本文提出的图像实值加密方法进行仿真，明文选用图2(a)所示的标准测试灰度图像Lena(图像尺寸为256×256)，对其进行基于分数阶Fourier变换的密钥参数为a=0.25，b=0.64，keyl=1043，key2；1021，得到的密文图像如图2(c)所示。

1、加密效果和统计特性分析

可见明文图像的直方图(图2(b))与相应密文图像的直方图(图2(d))具有明显的差别，这是因为在利用本文构造的保实分数阶Fourier变换进行实值加密变换后，明文与其相应的密文图像分别属于空域和变换域上，而不是在一个空间上的单纯置乱，因此它们的直方图具有明显的不同分布，也可以将这一现象理解为经典密码理论中的扩散，即将明文的统计特性扩散到整个空间，密文中的每一位均受明文多位的影响。在进行大量实验后还发现，不同的明文图像加密后的密文具有相似的直方图分布，与所使用的密钥是独立的，即完成了混淆，密码分析人员难以通过统计特性获得密钥信息，利用这一特点可以抵抗统计分析破泽，从而获得很好的安全性。

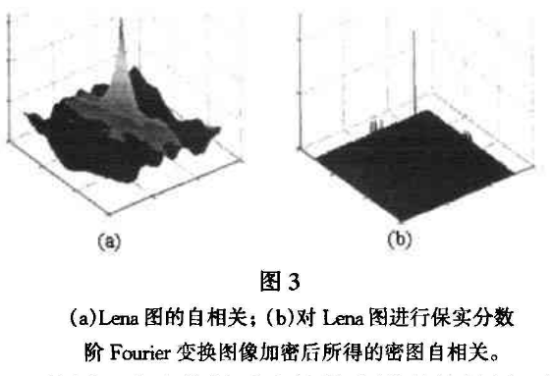
从图3中也能够看出扩散和混淆的效果。图3(a)是原始图像的自相关网格图，表明进行加密处理前，原始图像像素问的相关性很强；图3(b)是密图的自相关网格图，表明对原始图像进行加密后相邻像素间相关性很小，可见本算法具有很强的去相关能力，从而较好地完成了扩散和混淆，能对抗统计分析破译。图3(b)在水平和垂直方向上出现较小的相关是由于密图上的横竖条纹，但这并不妨碍图像的加密效果。

两幅图像的归一化互相关(Norrnalized Cross-Correlation) NC值被定义为：

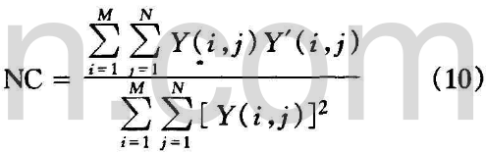
NC的取值区间为[0，1]。式中Y(i，j)和Y'(i，j)分别为两幅图像像素点的灰度值。为了说明密文图像具有类似白噪声的自相关性，这里使用本文提出的算法对Lena图像分别进行密钥为(0.25，0.64，1043，1021)和(0.42，0.51，1031，1051)的实值加密，计算得到的两份密图之间的NC值为0.0022，并且它们分别与原始Lena图像的值均为0.00240可见，对同一明文来说，由不同密钥产生的密文副本几乎不相关，每组明文密文对也是不相关的，验证了算法的加密效果。

2、算法的安全性测试和讨论

为了考察本文提出的图像实值加密算法的安全性，尝试使用不同密钥组合对同一个加密图像进行解密，图4是一些解密结果。

仿真中使用MSE(Mean Square Error)作为衡量解密图像质量的客观指标，图像态间的MSE可以定义成为式(10)，它可以直接反映出两幅图像在品质上的差异：

式中I(i，j)和H(i，j)分别表示原始图像和解密图像的像素点灰度值。当单个解密变换阶数密钥与正确密钥发生不同值的偏差时，计算解密图与原图的MSE，画出变换阶数偏差MSE曲线(图5)。正确解密密钥参数为（-0.25，-0.64，1043，1021）。

当使用正确密钥进行解密时，可无损地得到原始明文图像，四个密钥中的某一个稍有不匹配，将不能正确恢复明文图像(图4)。事实上，因为本文提出的加密算法足对称的，当密钥出错时，实际上是将密文图像又进行了一次全过程加密，变换到—个新的保实分数阶Fourier变换域上，因而使用了错误的密钥解密后，得到的还是杂乱的密文，而不会泄漏明文信息。

由阶数偏差MSE图（图5和图6）以及仿真试验可以看出，当解密时的单个阶数密钥误差达到0.02甚至更高的时候，将导致解密图像和原始图像有充分大的MSE，也就是说，当分数阶变换阶数被当作密钥的时候，其任意一个发生大于等于0.02的误差时将不能够正确解密，从而保护了数据的安全。在只有一个阶数密钥产生偏差的情况下，其误差小于0.02并且其它三个密钥都取正确值，只有这样才可能泄漏明文信息，但必须在置换矩阵种子密钥(key1，key2)已知的条件下才会发生，穷举置换矩阵种子也是一件相当困难的事情，这个特点使得穷举分析破译增加了难度。实际上：如果通过穷举来猜测算法中用到的置换矩阵的种子，当种子长度取64位时，以万亿次计算机的处理能力来计算，则穷举一个种子就需要58年，代价相当大；若直接穷举置换矩阵，所需要的计算量就更大。对于一幅256×256的明文图像来说，穷举一个置换矩阵需要256!8.6×10506次猜测，使用万亿次计算机需要8.6×10486年。可见本算法具有很好的安全性和抗穷举破译能力，在未经授权的情况下，想要得到明文几乎是不可能的。当然也可以通过使用另一组密钥进行二次加密来进一步提高抗穷举分析能力，即扩大密钥空间对抗穷举破译，本文讨论的是最简单的一次加密方法，未来工作将探讨算法的改进和结合。

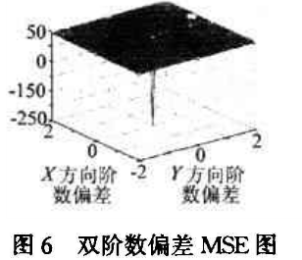
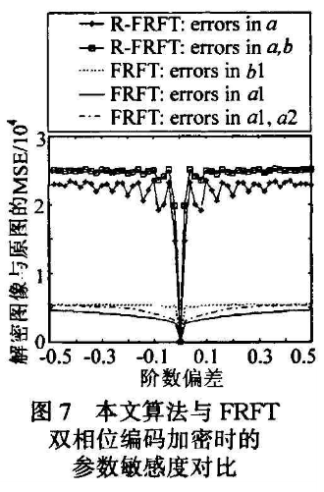
图7提出的基于分数阶Fourier变换的双相位编鸸加密方法与本文算法的阶数偏差MSE图，可见本算法对阶数的变化更加敏感，随着解密阶数偏差的增大，其解密图像与原图的MSE更迅速的上升。图7是一种利用分数阶Fourier变换和相位掩模进行图像加密的经典算法，其思想为众多基于分数阶Fourier变换的图像加密算法所借鉴，图中a1和b1分别是加密时x方向上第一次变换阶数和第二次变换阶数，a是加密时y方向上第一次变换阶数。此外需要再次强调的是，本文提出的算法得到的是一个实值密文图像，相比之下本文算法更适于进行数字图像加密，并且对密钥敏感度更高，更加安全。

3、算法的鲁棒性测试

首先对密文图像进行部分遮挡傅裁，然后再利用正确的密钥解密，仍然可以恢复出明文图像的大致信息（图8），可利用图像处理操作对这种情况下的解密图像质量进行改善。可见，算法对遮挡傅裁具有一定的鲁棒性。这也从另一个角度证实了前面章节中提到的扩散能力，在对图像进行网络传输时，在网络故障或者拥塞只能获得部分密文图像的情况下，利用本算法使用正确的密钥可以获得原始图像的大部分低频分量，从而可知晓明文信息。