为有效保护数字图像的安全,我们提出一种基于小波展开函数与超混沌系统的数字图像加密算法。这种图像加密算法利用小波展开函数对图像进行置乱通过超混沌系统扰乱原图像与加密图像文件之间的关系。
一、小波展开函数与超混沌系统
1、小波函数的展开
一个小波函数:
![]()
改变常系数k,系统的混沌特性就发生改变,随着k的增加,逐渐出现很多分岔,当k=1.25时,u在-0.5邻域内变化的时候出现了混沌现象。它的(u,y)分岔图与其他函数的迭代分岔图有很大的区别,随着u的增加,会出现1周期到2幂周期再到混沌,然后又从混沌中走出到2幂周期最后到1周期,中间出现了一些明显的奇数周期,正分岔与逆分岔完整地结合。
将式(1)中的小波函数进行泰勒展开后再经过改进,得到如下多项式函数式:
![]()
其中, 0.5<d<1.5; -1<c<0;k>1.28; 一1<μ<0;p为正有理数;floop(p)表示小于p的最大整数。
式(2)的多项式函数中具有5个参数,在上述给定的参数区间内,存在大量的混沌区域,由于这些区间基本上接近,这样给进行搜索可用参数的程序设计提供了方便。
事实上,多项式函数有很多是混沌的。另外,容易证明,单位区域上的曲线只要满足一定条件就是Li-Yorke混沌或者Devaney混沌,而参数的小幅度变化并没有更多的改变曲线的位置与形状,式(2)正是利用这些理论而构造的。
2、超混沌系统的四阶Runge-Kutta公式
在提出的加密方案中,一种新的超混沌系统从Chen混沌系统演变而来。超混沌Chen系统是四维混沌系统,其动力学方程式如下:
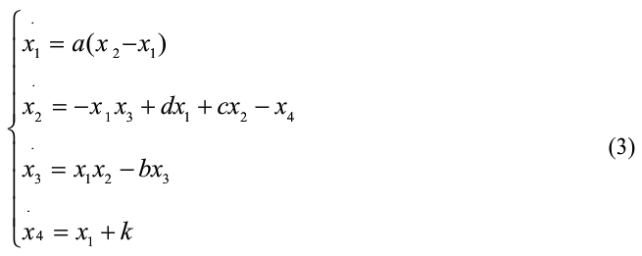
在式(3)中,当a=36,b=3,c=28,d=-16,-0.7≤k≤0.7时,系统处于超混沌状态。当k= 0.2时,系统Lyapunov指数为λ1= -12.573,λ2 =0,λ3=0.023,λ4 =1.522,超混沌系统有2个正的Lyapunov指数,拥有更为复杂的行为,随机性更强,因此,将超混沌系统用于图像加密,能大幅度提升系统的抗破译能力。
在构造混沌序列时使用四阶Runge-Kutta公式,在该式的中间过程插入参数,如式(4)所示:
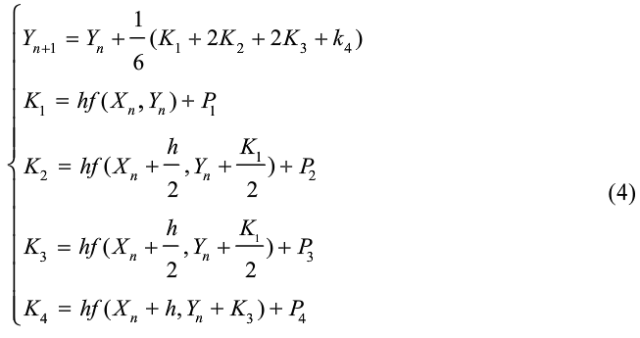
由于式(3)包含4个表达式,因此K1,K2,K3,K4,Xn,Yn,Yn+1,P1,P2,P3,P4都含有4个元素(P1,P2,P3,P4是后加入到Runge-Kutta公式中的),共计16个元素。
研究表明,一个混沌系统多数是在其混沌状态的某些参数区间内逐渐向非混沌过渡,这就为混沌加密提供了一定的密钥空间,而在四阶Runge-Kutta公式中插入的这些参数也都可以扩大密钥空间。实验分析表明这种插入参数的方法是可行的。在众多的参数空间中,其超混沌特性(即有2个正的Lyapunov指数)不变。
由于步长h很小,因此加在每个表达式上的参数p经过计算后变得很小,这样就相当于每一个曲面(或者几何体)向上或者向下作微小移动,根据研究的结果,多数情形下变换后的系统还是混沌的,但由于改变了(常数)参数,在相同初始值与相同参数的情形下,其生成的混沌序列不同,这就相当于扩大了密钥空间。
二、图像文件加密方案
图像文件加密过程包含2个部分:图像像素置乱过程和图像像素值的替换过程。
1、置乱过程
由于数字图像相邻的像素之间具有高度的相关性,为降低像素之间的相关性,采用小波函数展开式(2)进行迭代,产生混沌序列用来置换像素的位置。设原图像P,大小为M×N,P(i,j)表示图像的像素灰度值,i=1,2,L,M,j=l,2,L,N。
置乱过程描述如加密算法1所示。
加密算法1使用小波展开函数置乱图像的算法
(1)在初始化参数后,计算式(2)迭代序列的近似Lyapunov指数,如果Lyapunov指数小于0,更换参数,继续步骤(1),大于0,向下执行程序。
(2)通过式(2)迭代得到混沌实值序列:
![]()
上述序列用于行变换;如果在这个混沌序列中不存在相同迭代点,就进行步骤(3),反之,则去掉序列中的相同元素(所谓相同,规定好差值小于一定数值,软件的取舍精度也要有规定),继续迭代,续加补够M个元素(这样会获得较好的加密效果)。
(3)在步骤(1)所确定的初始化参数的邻域内更换新的初始化参数(是否重新计算近似Lyapunov指数根据具体情况决定),迭代得到序列(用于列变换),使用前2步的方法,得到没有重复值的混沌实值序列:
![]()
(4)将式(5)实值混沌序列和式(6)实值混沌序列中元素由小到大排序,分别形成有序序列s1,S2,L,SM和k1,k2,L,kN。
(5)分别确定式(5)混沌序列和式(6)混沌序列中的每个m(i)和n(j)分别在有序序列s1,S2,L,SM和k1,k2,L,kN中的位置编号,形成置换地址集合T={t1,t2,L,tM)和P={p1,p2,L,pN}。
(2)按置换地址集合丁和P对原始图像的像素进行置换,得到置乱后的位置矩阵E(i,j)。
对原图像文件完成置乱后,破坏了原像素的相邻像素点的相关性,但是像素点的灰度并没有改变,即图像直方图并没有发生变化,图像的加密效果不太理想叼因此,为提高图像文件加密的效果,使用下节中的替换过程对置乱后的图像的像素灰度进行改变。
2、替换过程
使用超混沌系统产生的混沌序列对置乱后的图像像素灰度值进行加密。替换过程如加密算法2所示。
加密算法2使用超混沌系统(替换)加密图像的算法
(1)把置乱后二维图像矩阵E(i,j)转化为一维序列A(i),i=1,2,L,M×N。
(2)计算参数的混沌区域,在该区域内给各个参数赋值,给定迭代初始值x1(0),x2 (0),x3(0),x4(0),超混沌陈系统(式(3))在四阶龙格一库塔法迭代式(式(4))作用下生成混沌序列
{x1(k),x2(k),x3(k),x4(k),k=1,2,L。对该混沌序列进行如下预处理:
![]()
其中,Abs(xi)表示xi的绝对值;函数Floor(z)表示小于z的最小整数;mod(x,y)表示x对y取余。
(3)通过d=mod(d,4),d∈[o,3],超混沌系统参数x1,x2,x3,x4不同结合状态如表1所示。

如果d等于序号组的序列,则选择相应的序列组执行加密操作。例如d=1,则选择(x1,x2,x3)用来进行加密。用序列A(i)数据的3 Byte和状态组数据的3 Byte做XOR(异或)操作。
通过以下公式进行计算:
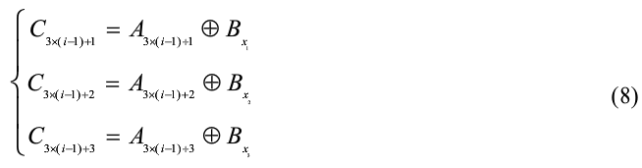
其中,i=1,2,…表示超混沌陈系统第f次迭代;+表示按位异或操作Bx1,Bx2,Bx3表示相应状态组的值;A表示置乱后序列A(i),i=1,2,L,M×N。
(4)继续上述操作,直到A={A1,A2,L,AM×N}中的所有像素值全部被加密为止。此时得到加密后像素集合为C={C1,C2,L,CM×N},然后将其转化为二维图像形式,得到了加密图像D(i,j)i=o,1,L,M一1,j=0,1,L,N-1。加密后的效果如图1(b)所示。

解密过程基本与加密过程的算法相似,是加密的逆操作过程。应首先由超Chen混沌系统进行解密对应于加密式(式(8)),解密所用的计算公式为:

将解密得到的序列么转换成二维矩阵形式;再用小波展开函数对解密矩阵进行反置乱,即可得到最后的解密图像,如图1(d)所示。
三、实验结果和安全性分析
1、密钥敏感性测试
为验证上述算法的有效性,本文以256×256的lena.bmp图像作实验测试图像。在本算法中初始参数也作为密钥。如果密钥稍有微小变化,如修改参数k=1.300 000 000 000 08(原k为1.3)加密效果如图1(c)所示,它与如图1(b)加密效果不同。经实验测试加密后的2幅图像中有99.06%的像素灰度值不相同。密钥的微小变化导致密文几乎完全不同,这就说明密钥的一点微小的变化将产生完全不同的加密效果,密钥敏感性高,因此,可以抗差分攻击。
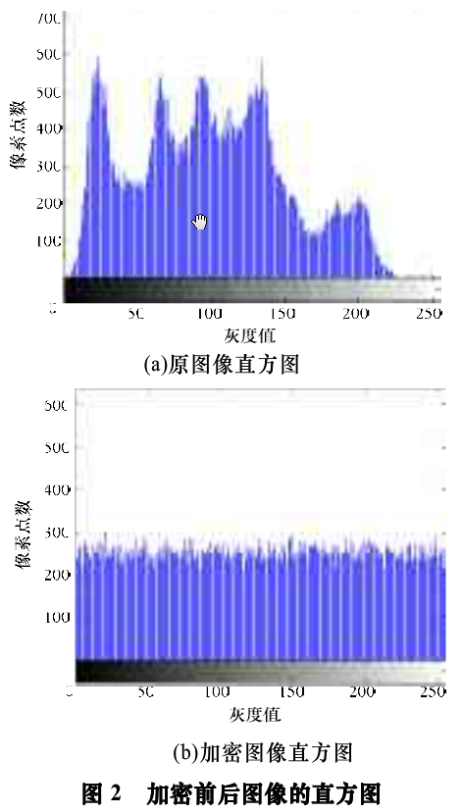
比较加密前后图像的直方图,如图2所示。可以看出,加密后图像的直方图与原始图像的直方图有很大的不同,并且非常均匀。变换后的直方图呈均匀分布,它掩盖了变换前分布规律,增加了破译的难度。
2、相邻像素的相关性分析
研究表明,图像置乱效果的好坏,与相邻像素相关性的大小存在反比关系:相关性越大,置乱效果越差;相关性越小,置乱的效果越好。为检验原始图像和密文图像相邻像素的相关性,从原图像和加密图像文件中随机选取4 000对相邻像素(水平、垂直或对角),利用下式计算其相邻像素的相关系数:
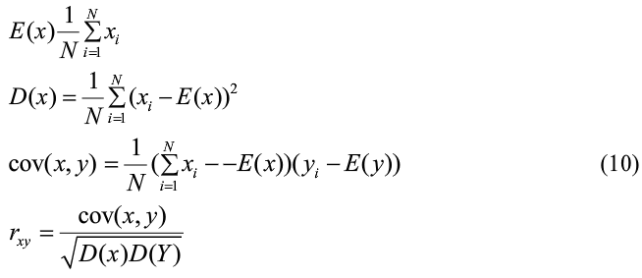
其中,x和y分别表示图像中相邻2个像素的灰度;rxy为相邻2个像素的相关系数。图3展示了原始图像和加密后图像的2个垂直方向的相邻像素的相关分布情况。
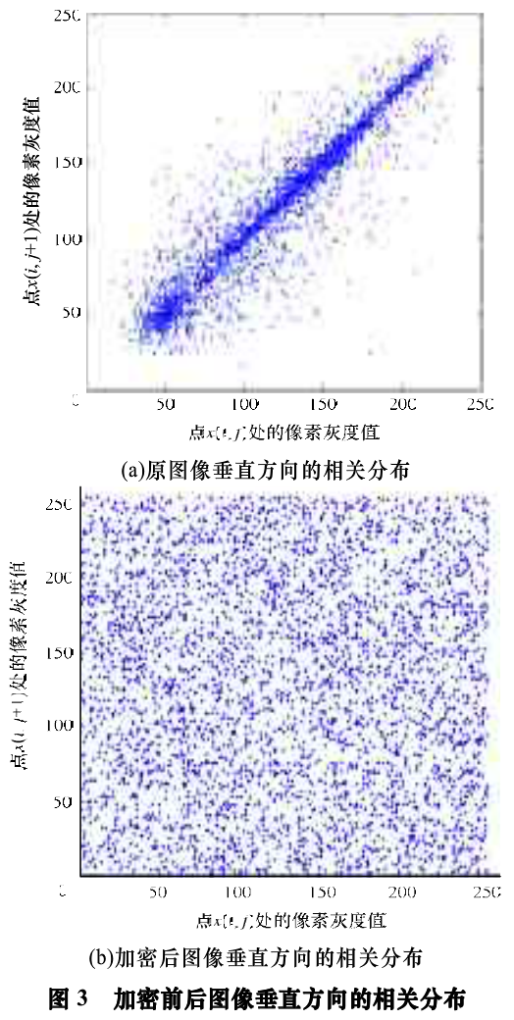
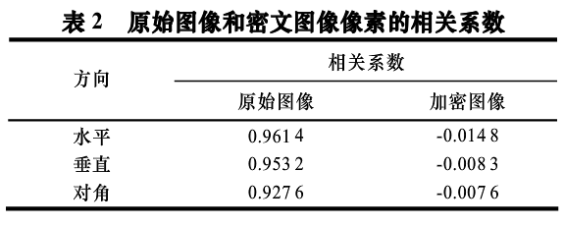
表2列出了加密前后各个方向的相关系数,可以看出,原始明文图像的相邻像素是高度相关的,相关系数接近于1,而加密图像的相邻像素相关系数比0还小,说明相邻像素不相关,明文的统计特性已被扩散到随机的密文中。
小知识之泰勒公式
在数学中,泰勒公式是一个用函数在某点的信息描述其附近取值的公式。如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。










