针对多变量三角形体制中Jonquieres映射的明密文之闻存在线性关系导致无法抵抗线性攻击的缺陷,我们研究了Jonquieres体制的中心映射中非线性扰动方法。通过将一维混沌Logistic映射及其同步反馈映射进行离散化后对Jonquieres体制的中心映射进行扰动,利用混沌序列的非线性特性,破坏明密文之问的线性关系,使线性攻击实施的先决条件不成立,以增强Jonquieres体制的安全性。
一、多变量三角形体制与Logistic混沌映射
1、多变量公钥密码体制
多变量公钥密码体制是建立在有限域上的多变量多项式,其数学结构如式(1)所示。
![]()
式(1)中,Fq是有限域,Fqn,Fqm均为Fq上的扩域(n,m为正整数),cijk,bij,ai∈ Fq,1≤i≤m。建立Fqn,Fqm上的仿射变换(如式(2)所示)和非线性变换f如式(3)所示)。
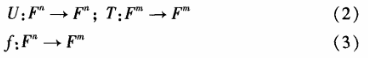
中心映射f由m个方程乃个变量构成,每个方程最高次数为2,如何构造具有良好密码性质的非线性可逆变换f是MPKC的核心。MPKC结构的另一种等价表达形式如式(4)所示:
![]()
多变量公钥密码体制的私钥由三部分组成:(U,F,T)。将y分解成U,F,T是一个IP问题,给定公钥y求解一组解髫称为MQ问题,多变量公钥密码体制基于这两个数学难题来构造单向陷门函数Y。目前,没有研究表明量子计算机在处理该问题上具有优势。
2、三角形体制
不同的中心映射的结构决定了不同类型的多变量公钥密码体制,其中三角形体制是比较特殊的一类,因为这一类体制的思想来源于代数几何。三角形体制有多种形式,其中最著名的可逆三角映射是Jonquibres提出的Jonquibres映射,其形式如式(5)所示。
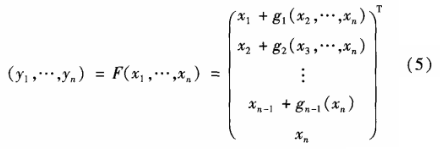
式(5)中,xi∈Fq;gi∈[xi,X2,...,xn];1≤i≤n是任意多项式。由于这种结构的特殊形式,该体制十分容易求逆,因此构造出的公钥体制即可以适用于签名,又可以用于加解密,且计算复杂度很低。但是从安全性的角度衡量,该体制由于满足线性化攻击而不能作为安全的密码算法。
3、混沌理论与Logistic映射
混沌之父Lorenz把混沌定义为“确定性系统的随机性行为”,混沌系统的输出具有很强的非线性特性,且参数和初始条件的微小变化都会使混沌序列的输出产生巨大的变化,对常规的密码分析方法有着很强的抗攻击能力,因此混沌序列以其唯一性、可靠性、类随机性和不可预测性等特点,很适合用于构造安全的密码体制。
根据方程中变量的个数,可将混沌方程分为一维、二维、三维混沌方程。混沌序列的产生方法有多种,如Logistic映射、Cat映射、Kent映射、Chebyshev映射等。其中一维Logistic映射的形式的表达式如式(6)所示:
![]()
式(6)中,Xn称为状态变量;μXn是驱动状态变量由Xn变化到Xn+1的驱动因素;μ为分又参数,当μ的值满足3. 569 945 6<μ≤4时,Logistic映射呈现混沌状态。logistic序列的遍历统计特性等同于零均值白 噪声,具有良好的随机性、相关性和复杂性,使得对混沌序列进行正确的长期预测不可能。
二、基于Logistic映射的多变量三角形加密体制
1、Logistic映射在有限域上的同步与离散化
Logistic映射的驱动系统如式(6)所示,受控系统如式(7)所示:
![]()
在受控系统中加人反馈控制项u(t),得到带反馈控制项的受控系统如式(8)所示:
![]()
同步化误差系统如式(9)所示:
![]()
设计同步反馈控制项u(t),使同步化误差en+1=0,实现驱动系统与受控系统的同步。一种反馈控制项如式(10)所示: 当运行时间t=17 s,即n>85时,驱动系统与受控系统达到同步。
![]()
进一步,将实值Logistic映射进行离散化,转换成有限域上的混沌系统。根据混沌序列{x1,…,xn,…|xi∈(O,1);i=l,2,..}的值,定义二进制序列{z1,…,zn,…,…|xi∈(O,1);i=l,2,..}如式(11)所示。
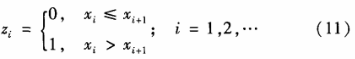
二、基于Logistic映射的多变量三角形密码体制
在Jonquieres映射中,设计适当的gi(xi+1,Xi+2,…,xn)(i=l,…,n-l),可以使明文xi与密文Yi(i=l,…,n-l)之间存在非线性关系,然而靠与Yn之间则存在着明显的线性关系,导致该三角形映射安全性受到严重威胁,也正因为如此,Jonquieres映射在提出后不久即被攻破。设计具有良好密码特征的三角形体制,必须消除明密文之间的线性关系。
确定有限域Fq和Fq上的多变量二次多项式gi(xi+1,Xi+2,…,xn)(i=l,…,n-l),建立可逆三角形Jonquibres映射如式(12)所示:
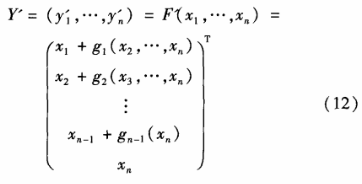
随机选取Logistic映射驱动系统初始值ro和分叉参数u(u >3. 569 945 6),建立Logistic映射如式(13)所示:
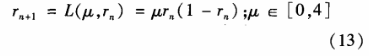
使用式(13)中的μ,随机选取受控系统初始值so,确定受控系统如式(14)所示,其中同步反馈项u(t)如式(14)。
![]()
求解同步化误差系统可得驱动系统与受控系统同步所需的最少时间t0和最少迭代次数n0。
任意选取整数N>n0,建立Fq上的Logistic扰动三角形加密体制如式(15)所示:
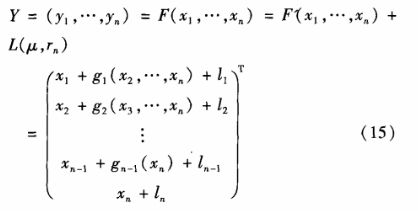
式(15)中,L(μ,rn)如式(13),{li,i =1,…,n}的值由L(μ,rn)离散化计算得到,如式(16)所示:
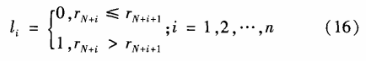
加密体制中加密密钥为(F’,ro,u,N),解密密钥为(F’, so,u,N)。
解密过程是加密的逆过程,根据so、u,首先计算式(14)所示的受控映射可得(s1,…,sN+n+1….),将si|i=l,…,N+n+1}离散化可得L’={li=1,…,n}如式(17)所示:
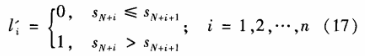
进一步,由密文Y=(yl,…,yn)和L’可计算得y’=(yl',…,yn')如式(18)所示:
![]()
最后,求解式(12)所示的Jonquibres映射的逆映射可得明文X=(x1,…,xn),求逆过程如式(19)所示:
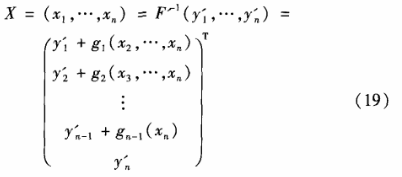
小知识之加密体制
也叫密码系统,是指能完整地解决信息安全中的机密性、数据完整性、认证、身份识别、可控性及不可抵赖性等问题中的一个或几个的一个系统。对一个密码体制的正确描述,需要用数学方法清楚地描述其中的各种对象、参数、解决问题所使用的算法等。







